Beta Distribution
beta_df <- tibble(
theta = seq(0, 1, by = 0.01),
p_theta = dbeta(theta, 4, 2)
)
beta_df %>% ggplot(aes(theta, p_theta)) + geom_line()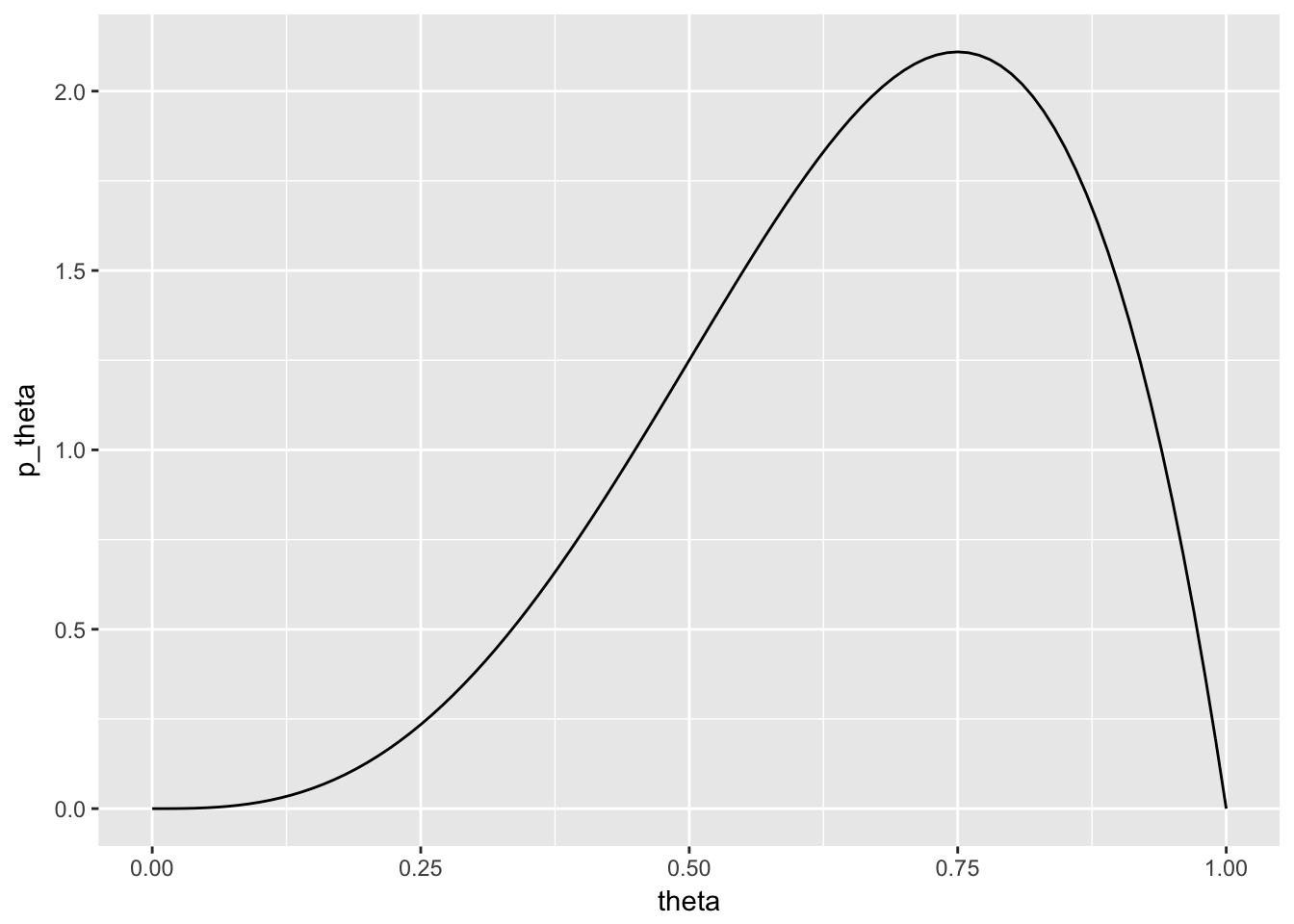
I define here a function bern_beta() that is similar to the author’s BernBeta(). This function assumes a beta prior with the prior parameters, \(a\) and \(b\) to be input along with the data parameters \(N\) and \(z\). The ouput is a faceted plot of the prior, likelihood, and posterior distributions.
bern_beta <- function(a, b, N, z) {
bern_beta_df <- tibble(
theta = seq(0, 1, by = 0.01),
prior = dbeta(theta, a, b), # beta prior
likelihood = theta ^ z * (1 - theta) ^ (N - z), # bernoulli likelihood
posterior = dbeta(theta, a + z, b + N - z) # beta posterior
)
# ouput is faceted plot of prior, likelihood, and posterior
cat("posterior beta parameters", a + z, b + N -z)
bern_beta_df %>%
gather(type, prob, -theta) %>%
mutate(type = factor(type, levels = c("prior", "likelihood", "posterior"))) %>%
ggplot(aes(theta, prob)) +
geom_line(col = "cornflowerblue") +
geom_area(fill = "cornflowerblue") +
facet_wrap(~type, ncol = 1, scales = "free")
}bern_beta(100, 100, 20, 17)## posterior beta parameters 117 103
bern_beta(18.25, 6.75, 20, 17)## posterior beta parameters 35.25 9.75
bern_beta(1, 1, 20, 17)## posterior beta parameters 18 4
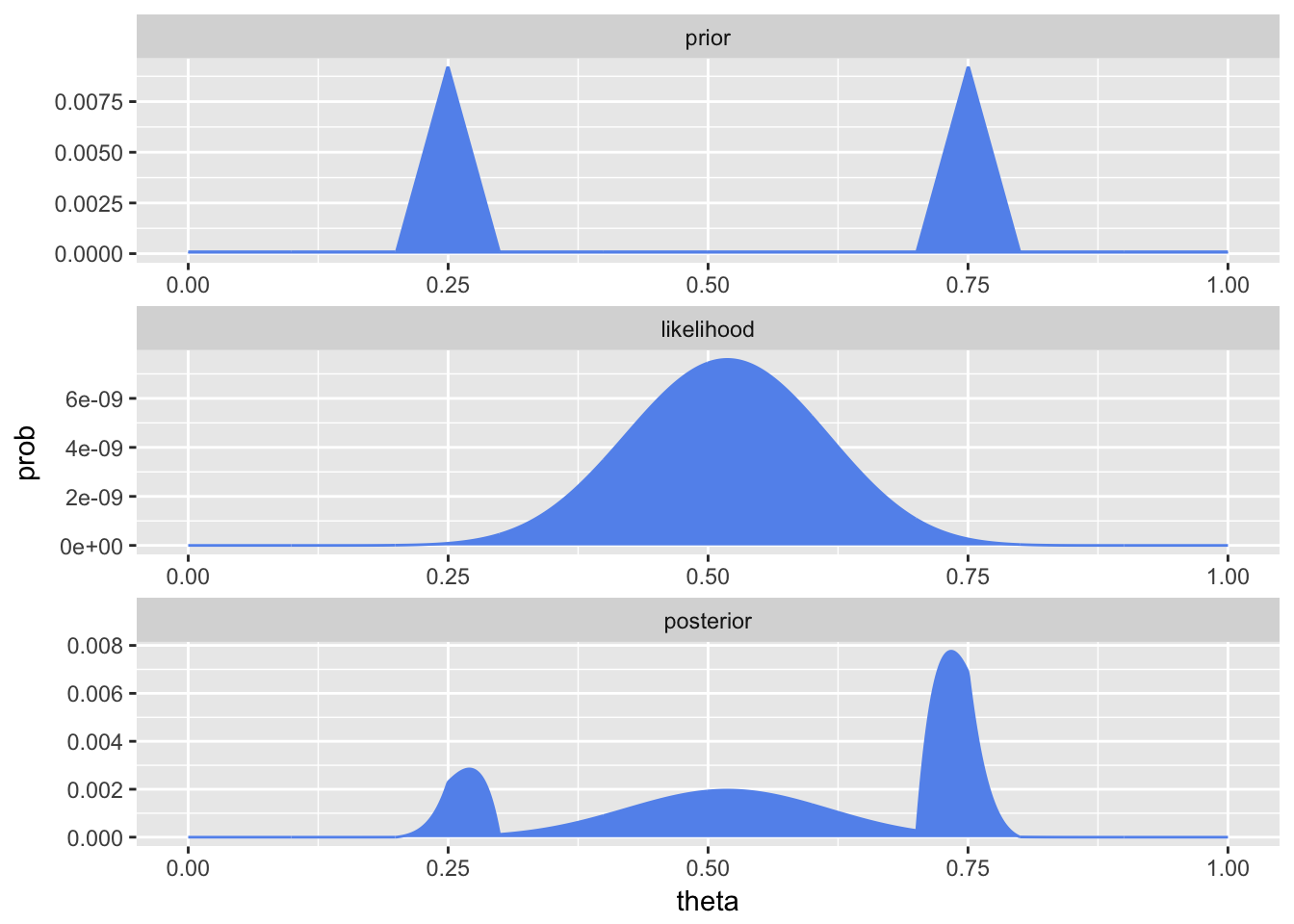
Non-beta prior
This reproduces Figure 6.5 in the text.
two_peak <- rep(c(rep(1, 200), seq(1, 100, length = 50), seq(100, 1, length = 50), rep(1, 200)),2)
coin_df <- tibble(
theta = seq(0, 1, length = 1000),
prior = two_peak / sum(two_peak),
likelihood = theta ^ 14 * (1 - theta) ^ (27 - 14),
posterior = prior * likelihood / sum(prior * likelihood)
)
# plot
coin_df %>%
gather(type, prob, -theta) %>%
mutate(type = factor(type, levels = c("prior", "likelihood", "posterior"))) %>%
ggplot(aes(theta, prob)) +
geom_line(col = "cornflowerblue") +
geom_area(fill = "cornflowerblue") +
facet_wrap(~type, ncol = 1, scales = "free")