Background
Sample Spaces and Events
An experiment is any action or process whose outcome is subject to uncertainty. The sample space of an experiment, denoted , is the set of all possible outcomes of that experiment. An event is any subset of .
Axioms of Probability
Let be a sample space, an event and a countable collection of pairwise disjoint events. Then,
Random Variable
Let be a sample space and let . Then is a random variable.
Example: For a coin toss we have . Let with and .
A random variable is a discrete random variable if its set of values is countable. A random variable is continuous if its set of values is an interval. (That’s not quite accurate, but it’s good enough.)
Probability Distributions
When probabilities are assigned to the outcomes in , these in turn determine probabilities associated with the values of any random variable defined on . The probability distribution of describes how the total probability of 1 is distributed among the values of .
Probability Mass Function (pmf)
Let be a discrete random variable. The probability mass function of (pmf) is the function such that for all , .
Example: The pmf for the random variable in the previous example where the probability of heads is is given by
Probability mass functions can be visualized with a line graph. For and :

It’s worth noting a couple of properties of a pmf:
Before moving on to continuous rv’s, a couple more examples.
Example: Consider the experiment of tossing a coin twice and counting the number of heads. Give the sample space, define a sensible random variable and draw a line graph for the pmf.
Solution: . Define by , and . Then the pmf is given by
ex1_df <- tibble(
x = c(0,1,2),
p_x = c(0.25, 0.5, 0.25)
)
ex1_df %>% ggplot(aes(x, p_x)) +
geom_col(width = 0.01) +
geom_point()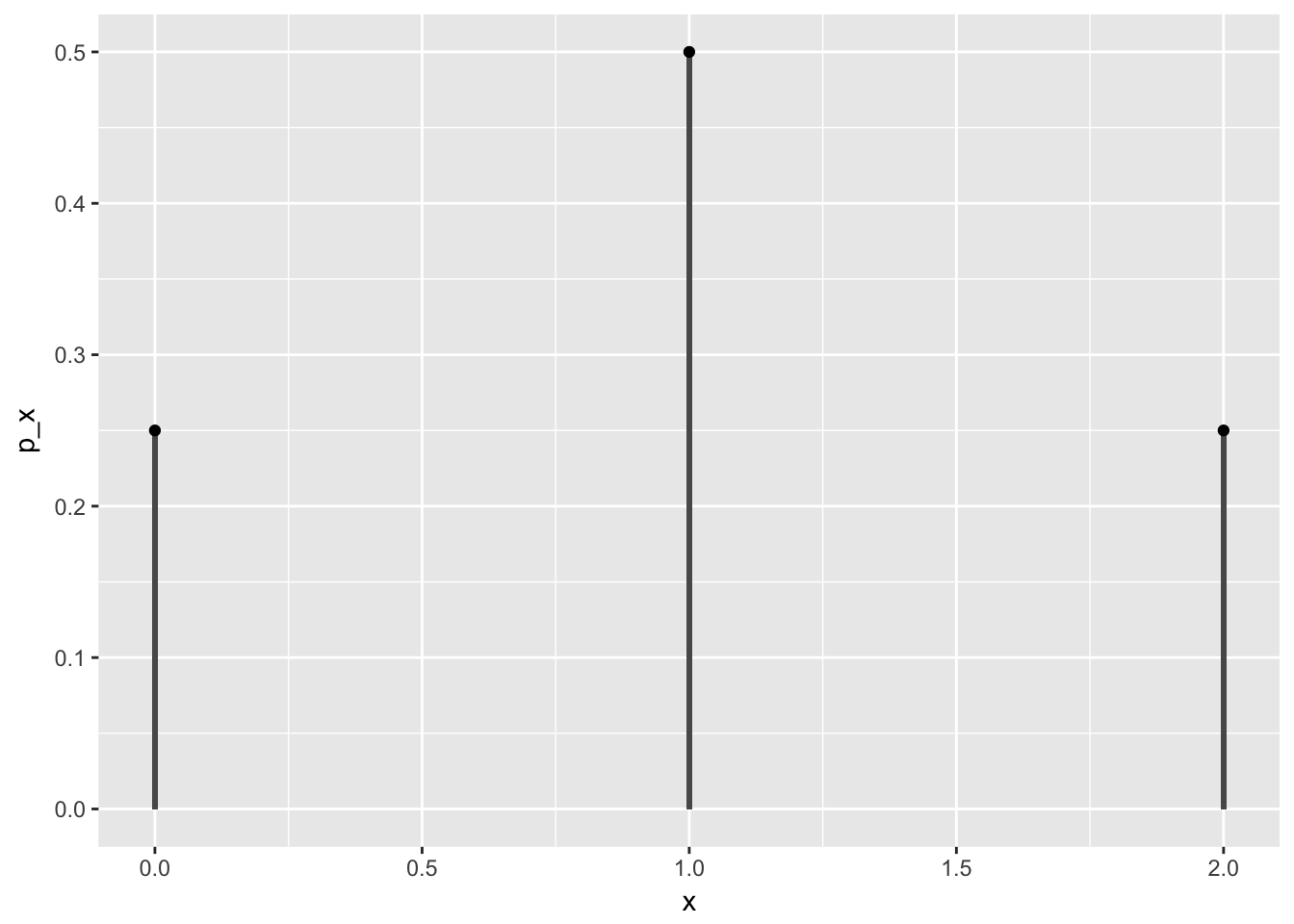
Example: Consider the experiment of tossing a biased coin (where the probability of heads is ) until it lands on heads. Give the sample space, define a sensible random variable and draw a line graph for the pmf.
Solution: . Define by the number of flips required. Then the pmf is given by
Probability Density Function (pdf)
Let be a continuous random variable. The probability density function of (pdf) is a function such that for ,
A couple of properties:
Example: A uniform random variable on is a model for “pick a random number between a and b.” The pdf is given by
Example: Let be normal random variable. Then has the pdf given by
where and are the mean and variance of . These are properties of that we now discuss.
Mean and Variance
Let be a random variable. The mean or expected value of is defined by
The variance of is given by
The expected value is often denoted and the variance, . The square root of the variance, , is called the standard deviation.
Highest density interval
The mean gives us one way to quantify the central tendency of a distribution. Variance is one way to quantify the spread of a distribution. Another way to quantify the spread of a distribution is to specify the highest density interval (HDI). The 95% HDI for a distribution, for example, is an interval such that for , for some fixed and
Using R to plot a normal random variable.
We include some code here for plotting the pdf shown on page 83 in the text. This is the pdf of a normal rv with mean 0 and standard deviation 0.2.
f <- function(x) (1 / sqrt(2 * pi * sig ^ 2)) * exp(-(x - mu) ^ 2 / 2 / sig ^ 2)
dx <- 0.01
x <- seq(-0.6, 0.6, by = dx)
mu <- 0
sig <- 0.2
plot(x, f(x), type = "l")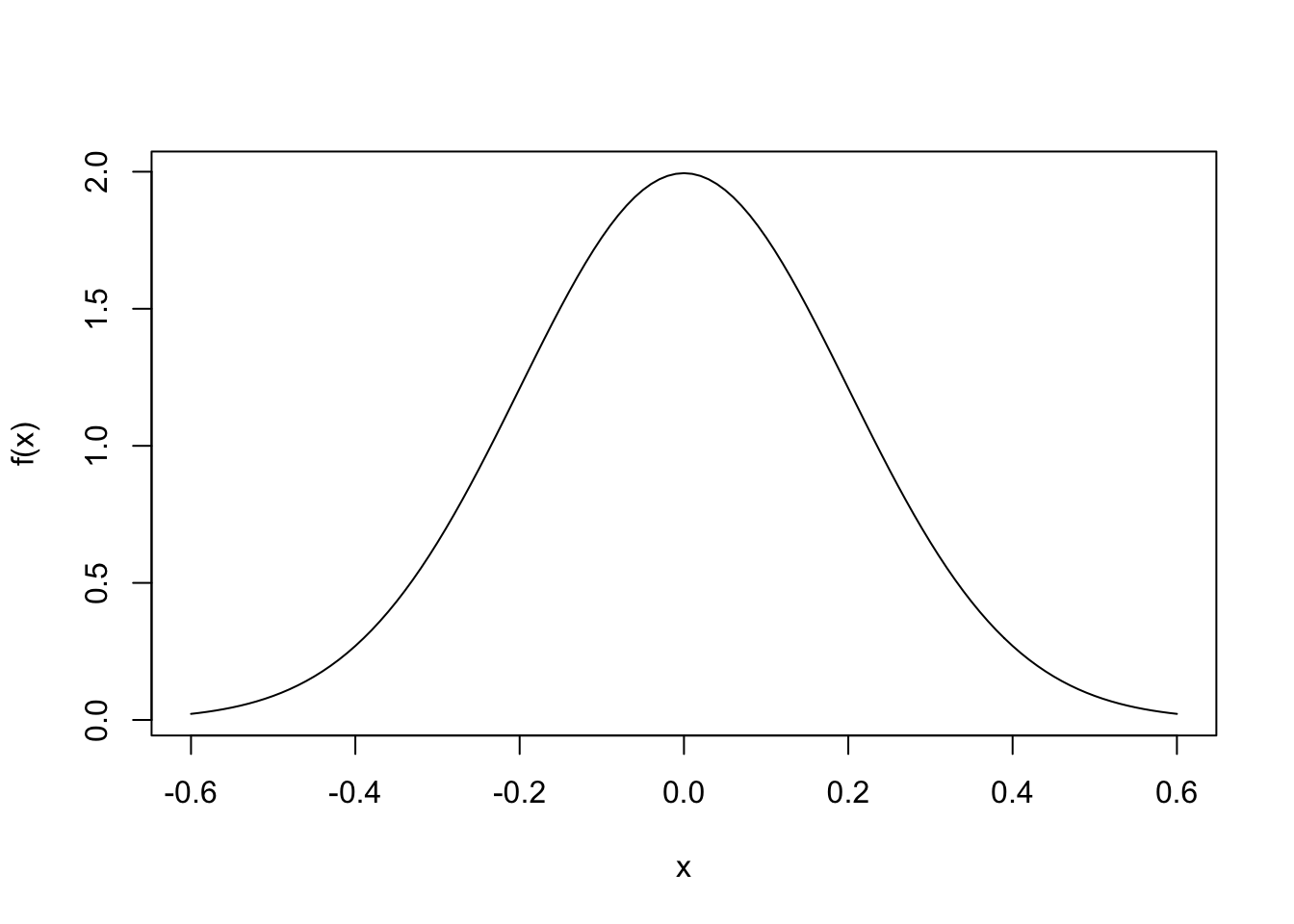
We can estimate the area under this curve. What should it be close to? Why?
sum(f(x)[-1]*dx)## [1] 0.9972947How much of the density is between and ?
sum(f(seq(-0.2, 0.2, by = dx))[-1]*dx)## [1] 0.6825887